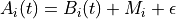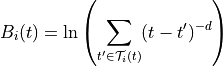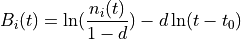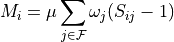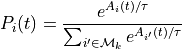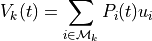PyIBL version 5.1.4

Introduction

PyIBL is a Python implementation of a subset of Instance Based Learning Theory (IBLT) [1]. It is made and distributed by the Dynamic Decision Making Laboratory of Carnegie Mellon University for making computational cognitive models supporting research in how people make decisions in dynamic environments.

Typically PyIBL is used by creating an experimental framework in the Python programming language, which uses one or more PyIBL Agent objects. The framework then asks these agents to make decisions, and informs the agents of the results of those decisions. The framework, for example, may be strictly algorithmic, may interact with human subjects, or may be embedded in a web site.

PyIBL is a library, or module, of Python code, useful for creating Python programs; it is not a stand alone application. Some knowledge of Python programming is essential for using it.

[1]

Cleotilde Gonzalez, Javier F. Lerch and Christian Lebiere (2003), Instance-based learning in dynamic decision making, Cognitive Science, 27, 591-635. DOI: 10.1016/S0364-0213(03)00031-4.

Installing PyIBL

The latest version of PyIBL can be downloaded and installed from PyPi with pip:

pip install pyibl

Use of a virtual environment for Python, such as venv or Anaconda is recommended.

PyIBL requires Python version 3.8 or later.

Note that PyIBL is simply a Python module, a library, that is run as part of a larger Python program. To build and run models using PyIBL you do need to do some Python programming. If you’re new to Python, a good place to start learning it is The Python Tutorial. To write and run a Python program you need to create and edit Python source files, and then run them. If you are comfortable using the command line, you can simply create and edit the files in your favorite text editor, and run them from the command line. Many folks, though, are happier using a graphical Integrated Development Environment (IDE). Many Python IDEs are available. One is IDLE, which comes packaged with Python itself, so if you installed Python you should have it available.

This document is also available at http://pyibl.ddmlab.com/.

Mailing list and reporting bugs

Users and others interested in PyIBL are encouraged to subscribe to the PyIBL Users mailing list.

The PyIBL community is small enough that this serves both as an announcement list and a discussion list. Announcements of new versions of PyIBL will be made here, and it is a good place to ask questions about PyIBL or to solicit other help in using it.

It is also a good place to report any bugs, or suspected bugs, in PyIBL. If, however, you would prefer not to report them to this list, please feel free to instead send them to Don Morrison.

Tutorial

Likely the easiest way to get started with PyIBL is by looking at some examples of its use. While much of what is in this chapter should be understandable even without much knowledge of Python, to write your own models you’ll need to know how to write Python code. If you are new to Python, a good place to start may be the Python Tutorial.

Note that when running the examples below yourself the results may differ in detail because IBL models are stochastic.

A first example of using PyIBL

In the code blocks that follow, lines the user has typed begin with any of the three prompts,

$
>>>
...

Other lines are printed by Python or some other command.

First we launch Python, and make PyIBL available to it. While the output here was captured in a Linux distribution and virtual environment in which you launch Python version 3.8 by typing python, your installation my differ and you may launch it with python3, py, or something else entirely; or start an interactive session in a completely different way using a graphical IDE.

$ python
Python 3.10.12 (main, Jun 11 2023, 05:26:28) [GCC 11.4.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> from pyibl import Agent

Next we create an Agent, named 'My Agent'.

>>> a = Agent(name="My Agent")
>>> a
<Agent My Agent 140441174486264>

We have to tell the agent what do if we ask it to choose between options it has never previously experienced. One way to do this is to set a default by setting the agent’s Agent.default_utility property.

>>> a.default_utility = 10.0

Now we can ask the agent to choose between two options, that we’ll just describe using two strings. When you try this yourself you may get the opposite answer as the IBLT theory is stochastic, which is particularly obvious in cases like this where there is no reason yet to prefer one answer to the other.

>>> a.choose(["The Green Button", "The Red Button"])
'The Green Button'

Now return a response to the model. We’ll supply 1.0.

>>> a.respond(1.0)

Because that value is significantly less than the default utility when we ask the agent to make the same choice again, we expect it with high probability to pick the other button.

>>> a.choose(["The Green Button", "The Red Button"])
'The Red Button'

We’ll give it an even lower utility than we did the first one.

>>> a.respond(-2.0)

If we stick with these responses the model will tend to favor the first button selected. Again, your results may differ in detail because of randomness.

>>> a.choose(["The Green Button", "The Red Button"])
'The Green Button'
>>> a.respond(1.0)
>>> a.choose(["The Green Button", "The Red Button"])
'The Red Button'
>>> a.respond(-2.0)
>>> a.choose(["The Green Button", "The Red Button"])
'The Green Button'
>>> a.respond(1.0)
>>> a.choose(["The Green Button", "The Red Button"])
'The Green Button'
>>> a.respond(1.0)
>>> a.choose(["The Green Button", "The Red Button"])
'The Green Button'
>>> a.respond(1.0)
>>> a.choose(["The Green Button", "The Red Button"])
'The Green Button'
>>> a.respond(1.0)

But doing this by hand isn’t very useful for modeling. Instead, let’s write a function that asks the model to make this choice, and automates the reply.

>>> def choose_and_respond():
...     result = a.choose(["The Green Button", "The Red Button"])
...     if result == "The Green Button":
...         a.respond(1.0)
...     else:
...         a.respond(-2.0)
...     return result
...
>>> choose_and_respond()
'The Green Button'

Let’s ask the model to make this choice a thousand times, and see how many times it picks each button. But let’s do this from a clean slate. So, before we run it, we’ll call reset() to clear the agent’s memory.

>>> a.reset()
>>> results = { "The Green Button" : 0, "The Red Button" : 0 }
>>> for _ in range(1000):
...     results[choose_and_respond()] += 1
...
>>> results
{'The Red Button': 11, 'The Green Button': 989}

As we expected the model prefers the green button, but because of randomness, does try the red one occasionally.

Now let’s add some other choices. We’ll make a more complicated function that takes a dictionary of choices and the responses they generate, and see how they do. This will make use of a bit more Python. The default utility is still 10, and so long as the responses are well below that we can reasonably expect the first few trials to sample them all before favoring those that give the best results; but after the model gains more experience, it will favor whatever color or colors give the highest rewards.

>>> def choose_and_respond(choices):
...     result = a.choose(choices)
...     a.respond(responses[result])
...     return result
...
>>> a.reset()
>>> responses = { "green": -5, "blue": 0, "yellow": -4,
...               "red": -6, "violet": 0 }
...
>>> choices = list(responses.keys())
>>> choices
['green', 'blue', 'yellow', 'red', 'violet']
>>> results = { k: 0 for k in choices }
>>> results
{'green': 0, 'blue': 0, 'yellow': 0, 'red': 0, 'violet': 0}
>>> for _ in range(5):
...     results[choose_and_respond(choices)] += 1
...
>>> results
{'green': 1, 'blue': 1, 'yellow': 1, 'red': 1, 'violet': 1}
>>> for _ in range(995):
...     results[choose_and_respond(choices)] += 1
...
>>> results
{'green': 10, 'blue': 488, 'yellow': 8, 'red': 8, 'violet': 486}

The results are as we expected.

Multiple agents

A PyIBL model is not limited to using just one agent. It can use as many as the modeler wishes. For this example we’ll have ten players competing for rewards. Each player, at each turn, will pick either 'safe' or 'risky'. Any player picking 'safe' will always receive 1 point. All those players picking 'risky' will share 7 points divided evenly between them; if fewer than seven players pick 'risky' those who did will do better than if they had picked 'safe', but if more than seven players pick 'risky' they will do worse.

>>> from pyibl import Agent
>>> agents = [ Agent(name=n, default_utility=20)
...            for n in "ABCDEFGHIJ" ]
>>> def play_round():
...     choices = [ a.choose(['safe', 'risky']) for a in agents ]
...     risky = [ a for a, c in zip(agents, choices) if c == 'risky' ]
...     reward = 7 / len(risky)
...     for a in agents:
...         if a in risky:
...             a.respond(reward)
...         else:
...             a.respond(1)
...     return (reward, "".join([ a.name for a in risky ]))

Here’s what running it for ten rounds looks like.

>>> for _ in range(10):
...     print(play_round())
...
(1.4, 'BDFHI')
(1.4, 'ACEGJ')
(1.75, 'DFGI')
(1.4, 'BDEHJ')
(0.875, 'ABCEFGHI')
(0.7777777777777778, 'ABCDFGHIJ')
(1.4, 'ACEFG')
(1.75, 'BHIJ')
(1.0, 'ACDEGHJ')

By just looking at a small sample of runs we can’t really discern any interesting patterns. Instead we’ll write a function that runs the agents many times, and gathers some statistics. We’ll work out how many agents pick risky, on average, by counting the length of the second value returned by play_round(); how many times each of the agents picked risky; and what the aggregate payoff was to each agent. And then run it for 1,000 rounds.

Note that before running it we get a clean slate by calling each agent’s reset method. And for the payoffs we round the results to one decimal place, as Python by default would be showing them to about 16 decimal places, and we don’t need that kind of precision.

>>> from statistics import mean, median, mode
>>> from itertools import count
>>> def run_agents(rounds):
...     for a in agents:
...         a.reset()
...     by_round = []
...     by_agent = [0]*len(agents)
...     agent_payoffs = [0]*len(agents)
...     for _ in range(rounds):
...         payoff, chose_risky = play_round()
...         by_round.append(len(chose_risky))
...         for a, i in zip(agents, count()):
...             if a.name in chose_risky:
...                 by_agent[i] += 1
...                 agent_payoffs[i] += payoff
...             else:
...                 agent_payoffs[i] += 1
...     print(mean(by_round), median(by_round), mode(by_round))
...     print(by_agent)
...     print([float(f"{p:.1f}") for p in agent_payoffs])
...
>>> run_agents(1000)
6.408 7.0 7
[856, 283, 681, 851, 313, 230, 874, 706, 820, 794]
[1106.2, 1001.0, 1056.5, 1097.7, 1004.9, 1001.8, 1102.2, 1052.7, 1092.1, 1076.9]

Note that this time when we ran it seven of the agents chose risky over two thirds of the time, but three, b, e and f, chose it less than one third of the time, but all received about the same reward over the course of 1,000 rounds, just a little better than if they’d all always chosen safe.

Let’s run it for a few more 1,000 round blocks.

>>> run_agents(1000)
6.483 6.0 6
[335, 884, 630, 472, 165, 875, 857, 706, 886, 673]
[1007.9, 1091.8, 1029.9, 1007.6, 1000.2, 1100.9, 1080.3, 1051.5, 1103.7, 1043.2]
>>> run_agents(1000)
6.476 7.0 7
[323, 318, 267, 299, 888, 847, 834, 902, 912, 886]
[1005.1, 1003.8, 1001.4, 1001.0, 1088.2, 1078.6, 1063.1, 1094.0, 1098.0, 1090.7]
>>> run_agents(1000)
6.455 6.0 6
[525, 572, 716, 558, 666, 707, 828, 641, 502, 740]
[1031.6, 1030.3, 1067.6, 1034.4, 1051.9, 1075.7, 1112.5, 1048.9, 1026.9, 1065.3]
>>> run_agents(1000)
6.408 7.0 7
[856, 283, 681, 851, 313, 230, 874, 706, 820, 794]
[1106.2, 1001.0, 1056.5, 1097.7, 1004.9, 1001.8, 1102.2, 1052.7, 1092.1, 1076.9]

We see that a similar pattern holds, with a majority of the agents, when seen over the full 1,000 rounds, having largely favored a risky strategy, but a minority, again over the full 1,000 rounds, having favored a safe strategy. But which agents these are, of course, varies from block to block; and, perhaps, if we looked at more local sequences of decisions, we might see individual agent’s strategies shifting over time.

Attributes

The choices an agent decides between are not limited to atomic entities as we’ve used in the above. They can be structured using “attributes.” Such attributes need to be declared when the agent is created.

As a concrete example, we’ll have our agent decide which of two buttons, 'left' or 'right', to push. But one of these buttons will be illuminated. Which is illuminated at any time is decided randomly, with even chances for either. Pushing the left button earns a base reward of 1, and the right button of 2; but when a button is illuminated its reward is doubled.

We’ll define our agent to have two attributes, "button" and "illuminatted". The first is which button, and the second is whether or not that button is illumiunated. In this example the the "button" value is the decision to be made, and "illuminatted" value represents the context, or situation, in which this decision is being made.

We’ll start by creating an agent, and two choices, one for each button.

>>> from pyibl import Agent
>>> from random import random
>>> a = Agent(["button", "illuminated"], default_utility=5)
>>> left = { "button": "left", "illuminated": False }
>>> right = { "button": "right", "illuminated": False }

While we’ve created them both with the button un-illuminated, the code that actually runs the experiment will turn one of them on, randomly.

>>> def push_button():
...     if random() <= 0.5:
...         left["illuminated"] = True
...     else:
...         left["illuminated"] = False
...     right["illuminated"] = not left["illuminated"]
...     result = a.choose([left, right])
...     reward = 1 if result["button"] == "left" else 2
...     if result["illuminated"]:
...         reward *= 2
...     a.respond(reward)
...     return result
...
>>> push_button()
{'button': 'right', 'illuminated': True}

Now we’ll reset the agent, and then run it 2,000 times, counting how many times each button is picked, and how many times an illuminated button is picked.

>>> a.reset()
>>> results = {'left': 0, 'right': 0, True: 0, False: 0}
>>> for _ in range(2000):
...     result = push_button()
...     results[result["button"]] += 1
...     results[result["illuminated"]] += 1
...
>>> results
{'left': 518, 'right': 1482, True: 1483, False: 517}

As we might have expected the right button is favored, as are illuminated ones, but since an illuminated left is as good as a non-illuminated right neither completely dominates.

Partial matching

In the previous examples experience from prior experiences only applied if the prior decisions, or their contexts, matched exactly the ones being considered for the current choice. But often we want to choose the option that most closely matches, though not necessarily exactly, for some definition of “closely.” To do this we define a similarity function for those attributes we want to partially match, and specify a mismatch_penalty parameter.

In this example there will be a continuous function, f(), that maps a number between zero and one to a reward value. At each round the model will be passed five random numbers between zero and one, and be asked to select the one that it expects will give the greatest reward. We’ll start by defining an agent that expects choices to have a single attribute, n.

>>> from pyibl import Agent
>>> from random import random
>>> import math
>>> import sys
>>> a = Agent(["n"])

We’ll define a similarity function for that attribute, a function of two variables, two different values of the attribute to be compared. When the attribute values are the same the value should be 1, and when they are maximally dissimilar, 0. The similarity function we’re supplying is scaled linearly, and its value ranges from 0, if one of its arguments is 1 and the other is 0, and otherwise scales up to 1 when they are equal. So, for example, 0.31 and 0.32 have a large similarity, 0.99, but 0.11 and 0.93 have a small similarity, 0.18.

>>> a.similarity(["n"], lambda x, y: 1 - abs(x - y))

The mismatch_penalty is a non-negative number that says how much to penalize past experiences for poor matches to the options currently under consideration. The larger its value, the more mismatches are penalized. We’ll experiment with different values of the mismatch_penalty in our model

Let’s define a function that will run our model, with the number of iterations, the mismatch_penalty, and the reward function supplied as parameters. Note that we reset the agent at the beginning of this function. We then supply one starting datum for the model to use, the value of the reward function when applied to zero. After asking the agent to choose one of five, randomly assigned values, our run_model function will work out which would have given the highest reward, and keep track of how often the model did make that choice. We’ll round that fraction of correct choices made down to two decimal places to make sure it is displayed nicely.

>>> def run_model(trials, mismatch, f):
...     a.reset()
...     a.mismatch_penalty = mismatch
...     a.populate([{"n": 0}], f(0))
...     number_correct = 0
...     fraction_correct = []
...     for t in range(trials):
...         options = [ {"n": random()} for _ in range(5) ]
...         choice = a.choose(options)
...         best = -sys.float_info.max
...         best_choice = None
...         for o in options:
...             v = f(o["n"])
...             if o == choice:
...                 a.respond(v)
...             if v > best:
...                 best = v
...                 best_choice = o
...         if choice == best_choice:
...             number_correct += 1
...         fraction_correct.append(float(f"{number_correct / (t + 1):.2f}"))
...     return fraction_correct

For our reward function we’ll define a quadratic function that has a single peak of value 5 when called on 0.72, and drops off on either side, down to 2.4 when called on 0 and down to 4.6 when called on 1.

>>> def f(x):
...    return 5 * (1 - math.pow(x - 0.72, 2))

Let’s first run it with a mismatch penalty of zero, which means all values will be considered equally good, and the result will simply be random guessing.

>>> run_model(100, 0, f)
[0.0, 0.0, 0.0, 0.25, 0.2, 0.17, 0.14, 0.25, 0.22, 0.2, 0.18,
 0.25, 0.31, 0.29, 0.27, 0.31, 0.29, 0.28, 0.26, 0.25, 0.24, 0.23,
 0.22, 0.21, 0.2, 0.19, 0.19, 0.18, 0.17, 0.2, 0.19, 0.19, 0.18,
 0.18, 0.17, 0.17, 0.19, 0.18, 0.18, 0.17, 0.17, 0.17, 0.16, 0.16,
 0.16, 0.15, 0.15, 0.15, 0.14, 0.14, 0.14, 0.13, 0.13, 0.13, 0.13,
 0.12, 0.14, 0.16, 0.15, 0.15, 0.15, 0.15, 0.16, 0.16, 0.15, 0.17,
 0.16, 0.16, 0.16, 0.16, 0.17, 0.17, 0.16, 0.16, 0.17, 0.17, 0.17,
 0.18, 0.18, 0.19, 0.19, 0.18, 0.18, 0.19, 0.19, 0.19, 0.18, 0.18,
 0.18, 0.18, 0.19, 0.18, 0.18, 0.18, 0.19, 0.2, 0.2, 0.2, 0.2, 0.2]

As we can see, it looks like random guessing, getting things right only about 20% of the time.

Now let’s try it with a mismatch penalty of 1, which won’t pay too much attention to how closely the values match those we’ve seen before, but will pay a little bit of attention to it.

>>> run_model(100, 1, f)
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.14, 0.12, 0.11, 0.1, 0.18, 0.25,
 0.31, 0.29, 0.27, 0.31, 0.29, 0.33, 0.32, 0.3, 0.29, 0.32, 0.35,
 0.33, 0.36, 0.35, 0.37, 0.36, 0.34, 0.33, 0.35, 0.34, 0.33, 0.32,
 0.34, 0.36, 0.35, 0.34, 0.36, 0.35, 0.37, 0.36, 0.35, 0.34, 0.36,
 0.37, 0.36, 0.35, 0.37, 0.36, 0.35, 0.37, 0.38, 0.39, 0.4, 0.41,
 0.4, 0.41, 0.41, 0.4, 0.39, 0.4, 0.41, 0.41, 0.42, 0.42, 0.42,
 0.43, 0.42, 0.41, 0.42, 0.42, 0.42, 0.42, 0.41, 0.42, 0.42, 0.41,
 0.41, 0.41, 0.41, 0.4, 0.4, 0.4, 0.41, 0.41, 0.4, 0.4, 0.39, 0.39,
 0.4, 0.4, 0.4, 0.4, 0.41, 0.42, 0.41, 0.42, 0.41, 0.42]

While it started out guessing, since it had only minimal information, as it learns more the model does much better, reaching correct answers about 40% of the time, twice as good a random.

If we use a much larger mismatch penalty, 30, we’ll see an even greater improvement, converging on being correct about 90% of the time.

>>> run_model(100, 30, f)
[0.0, 0.0, 0.33, 0.5, 0.6, 0.5, 0.57, 0.62, 0.67, 0.6, 0.55, 0.58,
 0.62, 0.64, 0.6, 0.62, 0.65, 0.67, 0.68, 0.7, 0.71, 0.68, 0.7,
 0.71, 0.72, 0.73, 0.74, 0.75, 0.76, 0.77, 0.77, 0.78, 0.79, 0.79,
 0.8, 0.81, 0.81, 0.82, 0.82, 0.82, 0.83, 0.83, 0.84, 0.84, 0.84,
 0.85, 0.85, 0.85, 0.86, 0.86, 0.86, 0.87, 0.87, 0.87, 0.87, 0.88,
 0.88, 0.88, 0.88, 0.88, 0.89, 0.89, 0.89, 0.89, 0.89, 0.89, 0.9,
 0.9, 0.88, 0.89, 0.89, 0.89, 0.89, 0.89, 0.89, 0.89, 0.9, 0.9,
 0.9, 0.9, 0.9, 0.89, 0.89, 0.89, 0.89, 0.9, 0.9, 0.9, 0.9, 0.9,
 0.9, 0.9, 0.9, 0.9, 0.91, 0.9, 0.9, 0.9, 0.9, 0.9]

Inspecting the model’s internal state and computations

Sometimes, possibly for debugging, possibly for writing detailed log files, and possibly for making unusual models, we want to be able to see what’s going on inside PyIBL. Several tools are provided to facilitate this.

The instances() method show’s all instances currently in an agent’s memory.

Consider this simple, binary choice model, that selects between a safe choice, always returning 1, and a risky choice which returns 2 fifty percent of the time, and 0 otherwise.

>>> a = Agent(default_utility=20)
>>> def run_once():
...     if a.choose(["safe", "risky"]) == "safe":
...         a.respond(1)
...     elif random() <= 0.5:
...         a.respond(2)
...     else:
...         a.respond(0)

If we run it once, and then look at its memory we see three instances, two that were created using the default_utility, and one actually experienced. As usual, if you run this yourself, it may differ in detail since PyIBL models are stochastic.

>>> run_once()
>>> a.instances()
+----------+---------+---------+-------------+
| decision | outcome | created | occurrences |
+----------+---------+---------+-------------+
|   safe   |    20   |    0    |     [0]     |
|  risky   |    20   |    0    |     [0]     |
|  risky   |    2    |    1    |     [1]     |
+----------+---------+---------+-------------+

Let’s run it ten more times and look again.

>>> for _ in range(10):
...     run_once()
...
>>> a.instances()
+----------+---------+---------+------------------+
| decision | outcome | created |   occurrences    |
+----------+---------+---------+------------------+
|   safe   |    20   |    0    |       [0]        |
|  risky   |    20   |    0    |       [0]        |
|  risky   |    0    |    1    |    [1, 8, 10]    |
|   safe   |    1    |    2    | [2, 5, 7, 9, 11] |
|  risky   |    2    |    3    |    [3, 4, 6]     |
+----------+---------+---------+------------------+

There are now five different instances, but all the actually experienced ones have been reinforced two or more times.

If we want to see how PyIBL uses these values when computing a next iteration we can turn on tracing in the agent.

>>> a.trace = True
>>> run_once()

safe → 1.6981119704016256
+------+----------+---------+------------------+---------+---------------------+----------------------+---------------------+-----------------------+
|  id  | decision | created |   occurrences    | outcome |   base activation   |   activation noise   |   total activation  | retrieval probability |
+------+----------+---------+------------------+---------+---------------------+----------------------+---------------------+-----------------------+
| 0132 |   safe   |    0    |       [0]        |    20   | -1.2424533248940002 |  0.6743933445745868  | -0.5680599803194134 |  0.036742735284296085 |
| 0135 |   safe   |    2    | [2, 5, 7, 9, 11] |    1    |  1.0001744608971734 | -0.41339471775300435 |  0.586779743144169  |   0.9632572647157039  |
+------+----------+---------+------------------+---------+---------------------+----------------------+---------------------+-----------------------+

risky → 0.23150913644216178
+------+----------+---------+-------------+---------+---------------------+----------------------+---------------------+-----------------------+
|  id  | decision | created | occurrences | outcome |   base activation   |   activation noise   |   total activation  | retrieval probability |
+------+----------+---------+-------------+---------+---------------------+----------------------+---------------------+-----------------------+
| 0133 |  risky   |    0    |     [0]     |    20   | -1.2424533248940002 | -0.2948777661505001  | -1.5373310910445004 | 0.0009256525969768487 |
| 0134 |  risky   |    1    |  [1, 8, 10] |    0    |  0.4111940833223344 | 0.48087038114494485  |  0.8920644644672793 |   0.8925763051517108  |
| 0136 |  risky   |    3    |  [3, 4, 6]  |    2    | 0.09087765648075839 | 0.049537460190590174 | 0.14041511667134857 |   0.1064980422513124  |
+------+----------+---------+-------------+---------+---------------------+----------------------+---------------------+-----------------------+

From this we see PyIBL computing blended values for the two options, safe and risky, of 1.6981 and 0.2315, respectively. For the former, it computed the activation of two relevant chunks, resulting in retrieval probabilities it used to combine the possible outcomes of 20 and 1, though heavily discounting the former because it’s activation is so low, because of decay. Similarly for the risky choice, though with three instances reflecting three outcomes in the agent’s memory.

To gain programmatic access to this data we can use the details of an agent. Here we run the model one more time and print the result details.

>>> from pprint import pp
>>> a.trace = False
>>> a.details = True
>>> run_once()
>>> pp(a.details)
[[{'decision': 'safe',
   'activations': [{'name': '0132',
                    'creation_time': 0,
                    'attributes': (('_utility', 20), ('_decision', 'safe')),
                    'reference_count': 1,
                    'references': [0],
                    'base_level_activation': -1.2824746787307684,
                    'activation_noise': 0.2343700698730416,
                    'activation': -1.0481046088577268,
                    'retrieval_probability': 0.0010536046644722481},
                   {'name': '0135',
                    'creation_time': 2,
                    'attributes': (('_utility', 1), ('_decision', 'safe')),
                    'reference_count': 6,
                    'references': [2, 5, 7, 9, 11, 12],
                    'base_level_activation': 1.184918357959952,
                    'activation_noise': 0.1904030286066936,
                    'activation': 1.3753213865666456,
                    'retrieval_probability': 0.9989463953355276}],
   'blended': 1.0200184886249728},
  {'decision': 'risky',
   'activations': [{'name': '0133',
                    'creation_time': 0,
                    'attributes': (('_utility', 20), ('_decision', 'risky')),
                    'reference_count': 1,
                    'references': [0],
                    'base_level_activation': -1.2824746787307684,
                    'activation_noise': -0.04867278847092464,
                    'activation': -1.331147467201693,
                    'retrieval_probability': 0.006544349628104761},
                   {'name': '0134',
                    'creation_time': 1,
                    'attributes': (('_utility', 0), ('_decision', 'risky')),
                    'reference_count': 3,
                    'references': [1, 8, 10],
                    'base_level_activation': 0.2724966041059383,
                    'activation_noise': 0.16088543930698337,
                    'activation': 0.43338204341292164,
                    'retrieval_probability': 0.9624144271846764},
                   {'name': '0136',
                    'creation_time': 3,
                    'attributes': (('_utility', 2), ('_decision', 'risky')),
                    'reference_count': 3,
                    'references': [3, 4, 6],
                    'base_level_activation': 0.027153555019573457,
                    'activation_noise': -0.8079194823991546,
                    'activation': -0.7807659273795811,
                    'retrieval_probability': 0.03104122318721878}],
   'blended': 0.1929694389365328}]]

We could use this information, for example, to write detailed log files of many iterations of our model while it runs over thousands of iterations.

Reference

PyIBL is an implementation of a subset of Instance Based Learn Theory (IBLT). The principle class is Agent, an instance of which is a cognitive entity learning and making decisions based on its experience from prior decisions, primarily by calls to its choose() and respond() methods. The decisions an agent is choosing between can be further decorated with information about their current state. There are facilities for inspecting details of the IBL decision making process programmatically facilitating debugging, logging and fine grained control of complex models.

class pyibl.Agent(attributes=[], name=None, noise=0.25, decay=0.5, temperature=None, mismatch_penalty=None, optimized_learning=False, default_utility=None, default_utility_populates=False, fixed_noise=False)

A cognitive entity learning and making decisions based on its experience from prior decisions. The main entry point to PyIBL. An Agent has a name, a string, which can be retrieved with the name property. The name cannot be changed after an agent is created. If, when creating an agent, the name argument is not supplied or is None, a name will be created of the form 'Anonymous-Agent-n', where n is a unique integer.

An Agent also has zero or more attributes, named by strings. The attribute names can be retrieved with the attributes property, and cannot be changed after an agent is created. Attribute names must be non-empty strings. The value of attributes, if present, should be an Iterable of strings. As a convenience if none of the attribute names contain spaces or commas a string consisting of the names, separated by commas or spaces may be used instead of a list.

The agent properties noise, decay, temperature, mismatch_penalty, optimized_learning, default_utility, default_utility_populates and fixed_noise can be initialized when creating an Agent.

name

The name of this Agent. It is a string, provided when the agent was created, and cannot be changed thereafter.

attributes

A tuple of the names of the attributes included in all situations associated with decisions this agent will be asked to make. These names are assigned when the agent is created and cannot be changed, and are strings. The order of them in the returned tuple is the same as that in which they were given when the agent was created.

choose(choices=None, details=False)

Selects which of the choices is expected to result in the largest payoff, and returns it.

The expected form of the choices depends upon whether or not this Agent has any attributes or not. If it does not, each of the choices should be a Hashable that is not None, representing an atomic choice; if any of the choices are not hashable or are None a ValueError is raised.

If this Agent does have attributes (that is, the attributes argument was supplied and non-empty when it was created, or, equivalently, the value of the attributes property is a non-empty list), then each of the choices can be either a Mapping, typically a dict, mapping attribute names to their values, or a Sequence, typically a list, containing attribute values in the order they were declared when this Agent was created and would be returned by attributes. Attributes not present (either there is no key in the Mapping, or a Sequence shorter than the number of attributes) have a value of None, while values not corresponding to attributes of the Agent (either a key in the Mapping that does not match an attribute name, or a Sequence longer than the number of attributes) are ignored. Whether a Mapping or a Sequence, all the attribute values must be Hashable, and are typically strings or numbers. If any of the choices do not have one of these forms a ValueError is raised.

In either case, if any pair of the choices duplicate each other, even if of different forms (e.g. dictionary versus list), and after adding default None values and removing ignored values, a ValueError is raised.

It is also possible to supply no choices, in which case those used in the most recent previous call to this method are reused. If there was no such previous call since the last time this Agent was reset() a ValueError is raised.

For each of the choices this method finds all instances in memory that match, and computes their activations at the current time based upon when in the past they have been seen, modified by the value of the decay property, and with noise added as controlled by the noise property. If partial matching has been enabled with mismatch_penalty such matching instances need not match exactly, and the similarities modified by the mismatch penalty are subtracted from the activations. If partial matching is not enabled only those instances that match exactly are consulted. “Exact” matches are based on Python’s == operator, not is. Thus, for example 0, 0.0 and False all match one another, as do 1, 1.0 and True.

Looking at the activations of the whole ensemble of instances matching a choice a retrieval probability is computed for each possible outcome, and these are combined to arrive at a blended value expected for the choice. This blending operation depends upon the value of the temperature property; if none is supplied a default is computed based on the value of the noise parameter. The value chosen and returned is that element of choices with the highest blended value. In case of a tie one will be chosen at random.

After a call to choose a corresponding call must be made to respond() before calling choose() again, or a RuntimeError will be raised.

If the details argument is also supplied and is True two values are returned as a 2-tuple, the first as above and the second containing data used to arrive at the selection. While the comparison of blended values used by choose() is the appropriate process for most models, for some specialized purposes the modeler may wish to implement a different decision procedure. This additional information, when combined with supplying a second argment to respond(), facilitates the construction of such more complicated models.

The second return value is a list of dicts, one for each choice. These dicts have entries for the choice, the blended value, and a list of retrieval probability descriptions. The retrieval probability descriptions are themselves dicts, one for each instance consulted in constructing the given choice’s blended value. Each of these latter dicts has two entries, one for the utility stored in the instance and the other its probability of retrieval.

Because of noise the results returned by choose are stochastic, so the results of running the following examples may differ in their details from those shown.

>>> from pprint import pp
>>> a = Agent(name="Button Pusher", default_utility=10)
>>> a.choose(["left", "right"])
'left'
>>> a.respond(5)
>>> a.choose()
'right'
>>> a = Agent(["species", "state"], "Pet Shop")
>>> a.populate([["parrot", "dead"]], 0)
>>> a.populate([["parrot", "squawking"]], 10)
>>> a.choose([["parrot", "dead"], ["parrot", "squawking"]])
['parrot', 'squawking']
>>> a = Agent(name="Cheese Shop")
>>> a.populate(["Tilset", "Wensleydale"], 10)
>>> a.choose(["Tilset", "Wensleydale"])
'Tilset'
>>> a.respond(1)
>>> choice, data = a.choose(["Tilset", "Wensleydale"], details=True)
>>> choice
'Wensleydale'
>>> pp(data)
[{'choice': 'Wensleydale',
  'blended_value': 10.0,
  'retrieval_probabilities': [{'utility': 10, 'retrieval_probability': 1.0}]},
 {'choice': 'Tilset',
  'blended_value': 2.1449539686120187,
  'retrieval_probabilities': [{'utility': 10,
                               'retrieval_probability': 0.12721710762355765},
                              {'utility': 1,
                               'retrieval_probability': 0.8727828923764424}]}]

respond(outcome=None, choice=None)

Provide the outcome resulting from the most recent decision selected by choose(). The outcome should be a real number, where larger numbers are considered “better.” This results in the creation or reinforcemnt of an instance in memory for the decision with the given outcome, and is the fundamental way in which the PyIBL model “learns from experience.”

By default the choice selected by choose() is the one to which the outcome is attached. In unusual cases, however, the modeler may prefer to select a different choice; for example, if using a different decision procedure based on the information returned by a True value of the second argument to Choose(), or if performing model tracing of an individual human’s behavior on the experiment being modeled. To support these unusual cases a second argument may be passed to respond(), which is the choice to actually be made. If it is not one of the choices provided in the original call to choose() a ValueError is raised.

It is also possible to delay feedback, by calling respond() without arguments, or with the first argument being None. This tells the Agent to assume it has received feedback equal to that it expected, that is, the blended value resulting from past experiences. In this case respond() returns a value, a DelayedRespone object, which can be used subsequently to update the response.

Warning

Delayed feedback is an experimental feature and care should be exercised in its use to avoid biologically implausible models.

If there has not been a call to choose() since the last time respond() was called a RuntimeError is raised. If outcome is neither None nor a real number a ValueError is raised.

populate(choices, outcome, when=None)

Adds instances to memory, one for each of the choices, with the given outcome, at the current time, without advancing that time. The outcome should be a Real number. The choices are as described in choose(). If provided, when should be a time, a dimensionless quantity, typically a count of the number of choose/respond cycles that have occurred since the agent was created or last reset(); providing time will cause the instances to be added at that specified time instead of the current time. The time provided may not be in the future.

This is typically used to enable startup of a model by adding instances before the first call to choose(). When used in this way the timestamp associated with this occurrence of the instance will be zero. Subsequent occurrences are possible if respond() is called with the same outcome after choose() has returned the same decision in the same situation, in which case those reinforcing occurrences will have later timestamps. An alternative mechanism to facilitate sartup of a model is setting the default_utility property of the agent. While rarely done, a modeler can even combine the two mechanisms, if desired.

It is also possible to call populate() after choose/respond cycles have occurred. In this case the instances are added with the current time as the timestamp. This is one less than the timestamp that would be used were an instance to be added by being experienced as part of a choose/respond cycle instead. Each agent keeps internally a clock, the number of choose/respond cycles that have occurred since it was created or last reset(). When choose() is called it advances that clock by one before computing the activations of the existing instances, as it must since the activation computation depends upon all experiences having been in the past. That advanced clock is the timestamp used when an instance is added or reinforced by respond().

The when argument, which if provided should be a time, can be used to add instances at other times.

Raises a ValueError if outcome is not a Real number, if any of the choices are malformed or duplicates, or if when is in the future.

Warning

In normal use you should only call populate() before any choose/respond cycles. If, for exotic purposes, you do wish to call it after, caution should be exercised to avoid biologically implausible models. It should not normally be necessary to use the when argument, which is provided only for esoteric uses. In particular instances may not be added in the future, as that would result in tears as operations such as choose() will raise an Exception.

default_utility

The utility, or a function to compute the utility, if there is no matching instance. If when choose() is called, for some choice passed to it there is no existing instance that matches the choice the value of this property is consulted. Note that an instance added with populate() counts as matching, and will prevent the interrogation of this property. If partial matching (mismatch_penalty) is enabled, any instance that even partially matches a choice will prevent the iterrogation of this property.

Warning

It is rarely appropriate to use default_utility when partial matching is being used. If they are used together the default_utility will only be applied the first time a relevant choice is made, as all subsequent choices will partially match. This generally gives unpredicatable results and is rarely useful. Instead, when using partial matching it is usually better to explicitly prepopulate appropriate instances using populate().

The value of this property may be a Real, in which case when needed it is simply used as the default utility. If it is not a Real, it is assumed to be a function that takes one argument, one of the choices passed to choose(). When a default utility is needed that function will be called, passing the choice in question to it, and the value returned, which should be a Real, will be used. If at that time the value is not a function of one argument, or it does not return a Real, a RuntimeError is raised.

The default_utility_populates property, which is False by default, controls whether or not an instance is added for each interrogation of the default_utility property. If an instance is added, it is added as by populate() at the current time.

Setting default_utility to None or False (the initial default) causes no default utility to be used. In this case, if choose() is called for a decision in a situation for which there is no instance available, a RuntimeError is raised.

default_utility_populates

Whether or not a default utility provided by the default_utility property is also entered as an instance in memory. This property has no effect if default_utility has been set to None or False.

reset(preserve_prepopulated=False)

Erases this agent’s memory and resets its time to zero. If it is True it deletes all those not created at time zero. IBLT parameters such as noise and decay are not affected. If False any prepopulated instances, including those created automatically if a default_utility is provided and default_utility_populates is True are removed, but the settings of those properties are not altered.

time

This agent’s current time. Time in PyIBL is a dimensionless quantity, typically just counting the number of choose/respond cycles that have occurred since the Memory was last reset().

advance(increment=1, target=None)

Advances the time of this agent by increment time steps. The increment, which defaults to 1, should be a non-negative integer; if it is not a ValueError is raised.

If target is provided instead of increment, it should be the future time to which to advance. If both target and increment are supplied the time is set to the later of target and the current time advanced by increment.

Returns the updated time.

A ValueError is raised if it is in the past or is not a non-negative integer.

noise

The amount of noise to add during instance activation computation. This is typically a positive, possibly floating point, number between about 0.2 and 0.8. It defaults to 0.25. If explicitly zero, no noise is added during activation computation. Setting noise to None or False is equivalent to setting it to zero.

If an explicit temperature is not set, the value of noise is also used to compute a default temperature for the blending operation on result utilities.

Attempting to set noise to a negative number raises a ValueError.

decay

Controls the rate at which activation for previously experienced instances in memory decay with the passage of time. Time in this sense is dimensionless, and simply the number of choose/respond cycles that have occurred since the agent was created or last reset(). The decay is typically between about 0.1 to about 2.0. The default value is 0.5. If zero memory does not decay. Setting decay to None or False is equivalent to setting it to zero. The decay must be less than 1 if this Agent is using optimized_learning. Attempting to set decay to a negative number raises a ValueError.

temperature

The temperature parameter used for blending values. If None, the default, the square root of 2 times the value of noise will be used. If the temperature is too close to zero, which can also happen if it is None and the noise is too low, or negative, a ValueError is raised.

mismatch_penalty

The mismatch penalty applied to partially matching values when computing activations. If None no partial matching is done. Otherwise any defined similarity functions (see similarity()) are called as necessary, and the resulting values are multiplied by the mismatch penalty and subtracted from the activation. For any attributes and decisions for which similarity functions are not defined only instances matching exactly on these attributes or decisions are considered.

Attempting to set this parameter to a value other than None or a non-negative real number raises a ValueError.

similarity(attributes=None, function=None, weight=None)

Assigns a function and/or corresponding weight to be used when computing the similarity of attribute values. The attributes are names of attributes of the Agent. The value of attributes, if present, should be an Iterable of strings. As a convenience if none of the attribute namess contain spaces or commas a string consisting of the names, separated by commas or spaces may be used instead of a list. For an Agent that has no attributes the attributes argument should be empty or omitted.

The function argument should be a Callable, taking two arguments, or True. The similarity value returned should be a real number between zero and one, inclusive. If True is passed as the value of function a default similarity function is used which returns one if its two arguments are == and zero otherwise. If, when called, the function returns a number outside that range a RuntimeError is raised. If, when the similarity function is called, the return value is not a real number a ValueError is raised.

The weight should be a positive, real number, and defaults to one.

Similarity functions are only called when the Agent has a mismatch_penalty specified. When a similarity function is called it is passed two arguments, attribute values to compare. The function should be commutative; that is, if called with the same arguments in the reverse order, it should return the same value. It should also be stateless, always returning the same values if passed the same arguments. If either of these constraints is violated no error is raised, but the results will, in most cases, be meaningless.

If one of function or weight is omitted but the other is supplied, the supplied item is set with the omitted one unchanged. If called with neither function nor weight the similarity function is removed.

In the following examples the height and width are assumed to range from zero to ten, and similarity of either is computed linearly, as the difference between them normalized by the maximum length of ten. The colors pink and red are considered 50% similar, and all other color pairs are similar only if identical, with the similarity weighted half as much as the usual default.

>>> a.similarity(["height", "width"], lambda v1, v2: 1 - abs(v1 - v2) / 10)
>>> def color_similarity(c1, c2):
...     if c1 == c2:
...         return 1
...     elif c1 in ("red", "pink") and c2 in ("red", "pink"):
...         return 0.5
...     else:
...         return 0
...
>>> a.similarity("color", color_similarity, 0.5)

optimized_learning

Whether or not this Agent uses the optimized_learning approximation when computing instance activations. If False, the default, optimized learning is not used. If True is is used for all cases. If a positive integer, that number of the most recent rehearsals of an instance are used exactly, with any older rehearsals having their contributions to the activation approximated.

Optimized learning can only be used if the decay is less than one. Attempting to set this parameter to True or an integer when decay is one or greater raises a ValueError.

The value of this attribute can only be changed when the Agent does not contain any instances, typically immediately after it is created or reset(). Otherwise a RuntimeError is raised.

Warning

Care should be taken when adjusting the time manually and using optimized learning as operations that depend upon activation may no longer raise an exception if they are called when advance has not been called after an instance has been created or reinforced, producing biologically implausible results.

discrete_blend(outcome_attribute, conditions)

Returns the most likely to be retrieved, existing value of outcome_attribute subject to the conditions. That is, the existing value from the instances in this Agent such that the likelihood one of those instances will be retrieved weighted by their probabilities of retrieval. The outcome_attribute should an attribute name in this Agent. The conditions should be a Mapping mapping attribute names to values, like the various choices provided to choose(). Also returns a second value, a dictionary mapping possible values of outcome_attribute to their probabilities of retrieval.

This method can be useful for building specialized models using schemes that do not correspond to the paradigm exposed by the usual choose/respond cycles.

instances(file=<_io.TextIOWrapper name='<stdout>' mode='w' encoding='utf-8'>, pretty=True)

Prints or returns all the instances currently stored in this Agent. If file is None a list of dictionaries is returned, each corresponding to an instance. If file is a string it is taken as a file name, which is opened for writing, and the results printed thereto; otherwise file is assumed to be an open, writable file. By default the file is standard out, typically resulting in the instances being printed to the console.

When printing to a file if pretty is true, the default, a format intended for reading by humans is used. Otherwise comma separated values (CSV) format, more suitable for importing into spreadsheets, numpy, and the like, is used.

details

A MutableSequence into which details of this Agent’s internal computations will be added. If None, the default, such details are not accumulated. It can be explicitly set to a MutableSequence of the modeler’s choice, typically a list, into which details are accumulated. Setting it to True sets the value to a fresh, empty list, whose value can be ascertained by consulting the value of details.

Warning

In complex models, or models with many iterations, the details can gather a lot of information quickly. It is often best to clear() or otherwise reset the details frequently.

A ValueError is raised if an attempt is made to set its value to anything other than None, True or a MutableSequence.

>>> from pprint import pp
>>> a = Agent(default_utility=10, default_utility_populates=True)
>>> a.choose(["a", "b", "c"])
'c'
>>> a.respond(5)
>>> a.details = True
>>> a.choose()
'a'
>>> pp(a.details)
[[{'decision': 'a',
   'activations': [{'name': '0000',
                    'creation_time': 0,
                    'attributes': (('_utility', 10), ('_decision', 'a')),
                    'references': (0,),
                    'base_activation': -0.3465735902799726,
                    'activation_noise': -0.1925212278297397,
                    'activation': -0.5390948181097123,
                    'retrieval_probability': 1.0}],
   'blended': 10.0},
  {'decision': 'b',
   'activations': [{'name': '0001',
                    'creation_time': 0,
                    'attributes': (('_utility', 10), ('_decision', 'b')),
                    'references': (0,),
                    'base_activation': -0.3465735902799726,
                    'activation_noise': -0.21036659990743722,
                    'activation': -0.5569401901874098,
                    'retrieval_probability': 1.0}],
   'blended': 10.0},
  {'decision': 'c',
   'activations': [{'name': '0002',
                    'creation_time': 0,
                    'attributes': (('_utility', 10), ('_decision', 'c')),
                    'references': (0,),
                    'base_activation': -0.3465735902799726,
                    'activation_noise': -0.0970213443277114,
                    'activation': -0.44359493460768396,
                    'retrieval_probability': 0.16296805894917318},
                   {'name': '0003',
                    'creation_time': 1,
                    'attributes': (('_utility', 5), ('_decision', 'c')),
                    'references': (1,),
                    'base_activation': 0.0,
                    'activation_noise': 0.1349273092778319,
                    'activation': 0.1349273092778319,
                    'retrieval_probability': 0.8370319410508268}],
   'blended': 5.814840294745866}]]

trace

A boolean which, if True, causes the Agent to print details of its computations to standard output. Intended for use as a tool for debugging models. By default it is False.

The output is divided into blocks, the first line of which describes the choice being described and the blended value of its outcome. This is followed by a tabular description of various intermediate values used to arrive at this blended value.

>>> a = Agent(default_utility=10, default_utility_populates=True)
>>> a.choose(["a", "b", "c"])
'b'
>>> a.respond(5)
>>> a.choose()
'a'
>>> a.respond(7.2)
>>> a.choose()
'c'
>>> a.respond(2.3)
>>> a.choose()
'a'
>>> a.respond(7.2)
>>> a.trace = True
>>> a.choose()

a → 7.214829206137316 @ time=5
+------+----------+---------+-------------+---------+---------------------+---------------------+---------------------+---------------------+-----------------------+
|  id  | decision | created | occurrences | outcome |   base activation   |   activation noise  |   total activation  |   exp(act / temp)   | retrieval probability |
+------+----------+---------+-------------+---------+---------------------+---------------------+---------------------+---------------------+-----------------------+
| 0006 |    a     |    0    |     [0]     |    10   | -0.8047189562170503 | 0.23439403910287038 | -0.5703249171141799 | 0.19926444531722448 |  0.00529614504904138  |
| 0010 |    a     |    2    |    [2, 4]   |   7.2   | 0.45574639440832615 |  0.8249453921296758 |  1.2806917865380019 |  37.425166810260265 |   0.9947038549509586  |
+------+----------+---------+-------------+---------+---------------------+---------------------+---------------------+---------------------+-----------------------+

b → 8.633125874767709 @ time=5
+------+----------+---------+-------------+---------+---------------------+----------------------+---------------------+----------------------+-----------------------+
|  id  | decision | created | occurrences | outcome |   base activation   |   activation noise   |   total activation  |   exp(act / temp)    | retrieval probability |
+------+----------+---------+-------------+---------+---------------------+----------------------+---------------------+----------------------+-----------------------+
| 0007 |    b     |    0    |     [0]     |    10   | -0.8047189562170503 | -0.16726717777620997 | -0.9719861339932603 |  0.063979539230306   |   0.7266251749535416  |
| 0009 |    b     |    1    |     [1]     |    5    | -0.6931471805599453 | -0.6244610552806152  | -1.3176082358405605 | 0.024070725797184517 |  0.27337482504645844  |
+------+----------+---------+-------------+---------+---------------------+----------------------+---------------------+----------------------+-----------------------+

c → 5.881552425492787 @ time=5
+------+----------+---------+-------------+---------+---------------------+--------------------+----------------------+--------------------+-----------------------+
|  id  | decision | created | occurrences | outcome |   base activation   |  activation noise  |   total activation   |  exp(act / temp)   | retrieval probability |
+------+----------+---------+-------------+---------+---------------------+--------------------+----------------------+--------------------+-----------------------+
| 0008 |    c     |    0    |     [0]     |    10   | -0.8047189562170503 | 0.5923008644042377 | -0.21241809181281257 | 0.548367776208054  |   0.4651366786354268  |
| 0011 |    c     |    3    |     [3]     |   2.3   | -0.3465735902799726 | 0.1835398166993702 | -0.1630337735806024  | 0.6305712354751412 |   0.5348633213645733  |
+------+----------+---------+-------------+---------+---------------------+--------------------+----------------------+--------------------+-----------------------+

'b'

aggregate_details

A Pandas DataFrame aggregating information about the computations performed by this Agent. Set to True to begin aggregating information, or to False (the default) to not collect this information. If already collecting information setting this to True will clear the already gathered information and start over.

This collecting of information is most useful if the Agent is used in a common pattern: a number of rounds of a task are performed, each round a choose/respond cycle, and this sequence of rounds is repeated over a number of distinct, virtual participants, reset() being called between each participant.

Each row of the resulting DataFrame corresponds to the state of one of the instances in the Agent at a particular time for a particular virtual participant. The columns in the DataFrame are

iteration

the number of times reset() has been called before recording the data in this row, which is typically an identifier for the virtual participant

time

the time in this Agent at which the data in this row was recorded, typically the round of the task

choice

the choice made in this round; if this Agent has attributes, the choice will be a tuple containing the values of the attributes in the order in which the attributes were declared when creating the Agent

utility

the utility in this instance

option

the option in this instance; note that this typically differs from the choice column as the choice is the choice made at this time while the option is the option in this instance, whether or not this instance contributed to the “winning” choice; however, as with choice, if the Agent was defined to have attributes the value in this column will be a tuple listing the values of those attributes in the order provided when the Agent was defined

blended_value

the blended value computed for the option in this instance at this time; note that the same blended value is reported for each row corresponding to an instance with the same option at the same time and iteration

retrieval_probability

the probability of retrieval of this instance at this time

activation

the activation of this instance at this time

base_level_activation

the base level term of the activation computation at this time

activation_noise

the noise term of the activation computation at this time

If partial matching was used at least once in this Agent since the aggregate details started being record there will be additional columns following those above. The first, mismatch, is the total mismatch penalty for this instance for this query. After this there is one column for each attribute that was partially matched, the similarity value computed for this attribute.

Note that each time the aggregate_details attribute is queried a new DataFrame is created from an internal data structure. If you wish to modify a DataFrame and have those changes retained you need to retain this DataFrame.

Warning

Collecting aggregate_details incurs costs, both in space and time, and for large, complex models some thought may be needed to balance these costs against the value and convenience of the results.

>>> a = Agent()
>>> a.aggregate_details = True
>>> a.populate(["a", "b"], 2.2)
>>> for participant in range(100):
        a.reset(True)
        for round in range(60):
            choice = a.choose(["a", "b"])
            if choice == "a":
                a.respond(1)
            else:
                a.respond(2 if random.random() < 0.5 else 0)
>>> a.aggregate_details
       iteration  time choice  utility option  blended_value  retrieval_probability  activation  base_level_activation  activation_noise
0              1     1      a      2.2      a       2.200000               1.000000    0.091998               0.000000          0.091998
1              1     1      a      2.2      b       2.200000               1.000000   -0.233124               0.000000         -0.233124
2              1     2      b      1.0      a       1.479895               0.600088   -0.390199               0.000000         -0.390199
3              1     2      b      2.2      b       2.200000               1.000000    0.185066              -0.346574          0.531639
4              1     3      b      1.0      a       1.261019               0.782484   -0.352501              -0.346574         -0.005927
5              1     3      b      2.0      b       2.004449               0.977755    0.321220               0.000000          0.321220
6              1     4      b      1.0      a       1.026956               0.977537   -0.250698              -0.549306          0.298608
7              1     4      b      2.0      b       2.010839               0.945803    0.507820               0.534800         -0.026980
8              1     5      b      1.0      a       1.053339               0.955551    0.111650              -0.693147          0.804797
9              1     5      b      0.0      b       1.662770               0.169062   -0.211333               0.000000         -0.211333
...          ...   ...    ...      ...    ...            ...                    ...         ...                    ...               ...
11990        100    56      b      1.0      a       1.000052               0.999956    2.261437               2.175180          0.086257
11991        100    56      b      2.0      b       1.366890               0.683311    0.762205               0.813690         -0.051485
11992        100    57      a      1.0      a       1.000002               0.999998    2.427721               2.088158          0.339563
11993        100    57      a      2.0      b       0.422011               0.210943    0.814716               0.783826          0.030889
11994        100    58      b      1.0      a       1.000018               0.999985    2.148301               2.153508         -0.005207
11995        100    58      b      2.0      b       1.733465               0.866600    1.085368               0.756193          0.329175
11996        100    59      b      1.0      a       1.000011               0.999991    2.089526               2.077563          0.011963
11997        100    59      b      2.0      b       1.246271               0.623060    1.708573               0.730428          0.978145
11998        100    60      b      1.0      a       1.000004               0.999996    2.318136               2.026204          0.291932
11999        100    60      b      2.0      b       1.081265               0.540324    1.061905               1.107370         -0.045465
[12000 rows x 10 columns]

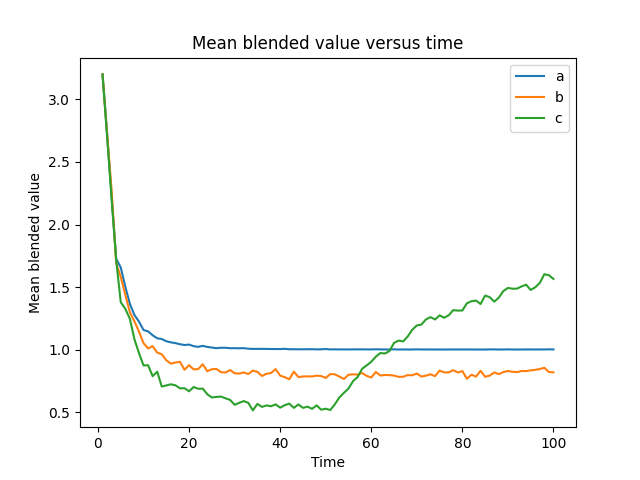
plot(kind, title=None, xlabel=None, ylabel=None, include=None, exclude=None, min=None, max=None, earliest=None, latest=None, legend=None, limits=None, filename=None, show=None)

Generates a variety of plots of the evolution of this Agent’s state over time. These plots can often be helpful in understanding how a PyIBL model is working. To generate these plots aggregate_details must be set to True. The constraints on the model for producing useful aggregate_details similarly apply for producing useful plots. Note that these plots are of values averaged over all the virtual participants. The kind argument to plot() should be a string, one of the following

"choice"

a plot of the number of times various choices are made by the model as a function of time

"bv"

a plot of the blended values of the options considered as a function of time

"probability"

a plot of the probabilities of retrieval of the various instances as a function of time

"activation"

a plot of the activations of the various instances as a function of time

"baselevel"

a plot of the base level term in the activation computations of the various instances as a function of time

"mismatch"

the total mismatch penalty terms in the activation computations of the various instances as a function of time

In addition, the kind may be a string comprised of the name of an attribute concatenated with ".similarity", which will produce a plot of the average similarity value of this attribute’s value to that sought as a function of time.

Whether or not the plot is displayed and/or saved to a file can be specified with the optional arguments show (a Boolean) and filename (a string). If show is not provided, by default the file will be displayed if and only if no filename is provided. In addition the plot is always returned by this method as a matplotlib Figure.

Details of the plot can be manipulated with several other optional arguments to plot():

title

the title applied to the plot

xlabel and ylabel

the labels of the corresponding axes of the plot

include*and *exclude

these should be lists of options; if include is provided only options in this list are displayed; any options in exclude are not displayed; if an option appears in both lists it is not displayed

min and max

these should be Real numbers; if min is supplied only results for instances with a utility greater or equal to this value are displayed; if max is supplied only results for instances with a utility less than or equal to this value are displayed

earliest and latest

these should be Real numbers; if earliest is supplied only results at this time or later are displayed; if latest is supplied only results at this time or earlier are displayed

legend

if True a legend is displayed on the plot; if False no legend is displayed; other values can also be supplied, which are passed on to matplotlib; by default a legend is shown only if there are not so many items in the plot that the legend would likely overflow the available space

limits

this should be a list or tuple of two Real numbers, the smallest and greatest values of the Y axis of the plot; if not supplied suitable defaults are assumed

Since plot() always returns a Figure, more sophisticated manipulations can be made of it and the result displayed explicitly.

>>> a = Agent()
>>> a.aggregate_details = True
>>> a.populate(["a", "b", "c"], 3.2)
>>> for participant in range(1000):
        a.reset(True)
        for round in range(100):
            choice = a.choose(["a", "b", "c"])
            if choice == "a":
                a.respond(1)
            elif choice == "b":
                a.respond(2 if random.random() < 1/2 else 0)
            elif a.time <= 50:
                a.respond(3 if random.random() < 1/3 else 0)
            else:
                a.respond(3 if random.random() < 2/3 else 0)
>>> a.plot("bv")

noise_distribution

Provide an alternative distribution from which noise is sampled. If None the default logistic distribution is used. Otherwise the value of this attribute should be a callable that takes no arguments and returns a real number. It will be called once each time activation noise is required and the value, scaled as usual by the noise parameter, will be used as the activation noise. A ValueError is raised if an attempt is made to set this attribute to anything other than a callable or None.

Warning

It is rarely appropriate to use noise_distribution. The default logistic distribution is almost always a more appropriate choice. The ability to change the distribution is provided only for esoteric purposes, and care should be exercised lest biologically implausible models result.

fixed_noise

Whether or not to constrain activation noise to remain constant at any one time. In some complicated models it may be necessary to compute the activation of an instance more than once at the same time step. Normally in this case each such computation generates its own, independent value of the activation noise. For some esoteric purposes it may be preferred to use the same activation noise for these different perspectives of an instance’s activation, which can be achieved by setting this property to True. By default fixed_noise is False.

class pyibl.DelayedResponse(agent, attributes, expectation)

A representation of an intermediate state of the computation of a decision, as returned from respond() called with no arguments.

is_resolved

Whether or not ground truth feedback to the Agent regarding this decision has yet been delivered by the user.

outcome

The most recent response learned by the Agent for this decision. When is_resolved is False this will be the reward expected by the Agent when the decision was made. After it has been resolved by calling update(), delivering the ground truth reward, this will be that real value.

expectation

The expected value learned when this DelayedReponse was created.

update(outcome)

Replaces the current reward learned, either expected or ground truth, by a new ground truth value.

The outcome is a real number. Typically this value replaces that learned when respond() was called, though it might instead replace the value supplied by an earlier call to update(). It is always learned at the time of the original call to respond().

The most recent previous value of the learned reward, either the expected value, or that set by a previous call of update(), is returned.

Raises a ValueError if outcome is not a real number.

Because of noise the results returned by choose are stochastic the results of running the following examples will differ in their details from those shown.

>>> a = Agent(default_utility=10, default_utility_populates)
>>> a.choose(["a", "b"])
'b'
>>> a.respond(2)
>>> a.choose()
'a'
>>> a.respond(3)
>>> a.choose()
'a'
>>> r = a.respond()
>>> a.choose()
'a'
>>> a.respond(7)
>>> a.instances()
+----------+-------------------+---------+-------------+
| decision |      outcome      | created | occurrences |
+----------+-------------------+---------+-------------+
|    a     |         10        |    0    |     [0]     |
|    b     |         10        |    0    |     [0]     |
|    b     |         2         |    1    |     [1]     |
|    a     |         3         |    2    |     [2]     |
|    a     | 8.440186635799552 |    3    |     [3]     |
|    a     |         7         |    4    |     [4]     |
+----------+-------------------+---------+-------------+
>>> r.update(1)
8.440186635799552
>>> a.instances()
+----------+---------+---------+-------------+
| decision | outcome | created | occurrences |
+----------+---------+---------+-------------+
|    a     |    10   |    0    |     [0]     |
|    b     |    10   |    0    |     [0]     |
|    b     |    2    |    1    |     [1]     |
|    a     |    3    |    2    |     [2]     |
|    a     |    1    |    3    |     [3]     |
|    a     |    7    |    4    |     [4]     |
+----------+---------+---------+-------------+

pyibl.positive_linear_similarity(x, y)

Returns a similarity value of two positive Real numbers, scaled linearly by the larger of them. If x and y are equal the value is one, and otherwise a positive float less than one that gets smaller the greater the difference between x and y.

If either x or y is not positive a ValueError is raised.

>>> positive_linear_similarity(1, 2)
0.5
>>> positive_linear_similarity(2, 1)
0.5
>>> positive_linear_similarity(1, 10)
0.09999999999999998
>>> positive_linear_similarity(10, 100)
0.09999999999999998
>>> positive_linear_similarity(1, 2000)
0.0004999999999999449
>>> positive_linear_similarity(1999, 2000)
0.9995
>>> positive_linear_similarity(1, 1)
1
>>> positive_linear_similarity(0.001, 0.002)
0.5
>>> positive_linear_similarity(10.001, 10.002)
0.9999000199960006

pyibl.positive_quadratic_similarity(x, y)

Returns a similarity value of two positive Real numbers, scaled quadratically by the larger of them. If x and y are equal the value is one, and otherwise a positive float less than one that gets smaller the greater the difference between x and y.

If either x or y is not positive a ValueError is raised.

>>> positive_quadratic_similarity(1, 2)
0.25
>>> positive_quadratic_similarity(2, 1)
0.25
>>> positive_quadratic_similarity(1, 10)
0.009999999999999995
>>> positive_quadratic_similarity(10, 100)
0.009999999999999995
>>> positive_quadratic_similarity(1, 2000)
2.4999999999994493e-07
>>> positive_quadratic_similarity(1999, 2000)
0.9990002500000001
>>> positive_quadratic_similarity(1, 1)
1
>>> positive_quadratic_similarity(0.001, 0.002)
0.25
>>> positive_quadratic_similarity(10.001, 10.002)
0.9998000499880025

pyibl.bounded_linear_similarity(minimum, maximum)

Returns a function of two arguments that returns a similarity value reflecting a linear scale between minimum and maximum. The two arguments to the function returned should be Real numbers between minimum and maximum, inclusive. If the two arguments to the function returned are equal they are maximally similar, and one is returned. If the absolute value of their difference is as large as possible, they are maximally different, and zero is returned. Otherwise a scaled value on a linear scale between these two extrema, measuring the magnitude of the difference between the arguments to the returned function is used, a value between zero and one being returned.

Raises a ValueError if either minimum or maximum is not a Real number, or if minimum is not less than maximum.

When the returned function is called if either of its arguments is not a Real number a ValueError is then raised. If either of those arguments is less than minimum, or greater than maximum, a warning is issued, and either minimum or maximum, respectively, is instead used as the argument’s value.

>>> f = bounded_linear_similarity(-1, 1)
>>> f(0, 1)
0.5
>>> f(-0.1, 0.1)
0.9
>>> f(-1, 1)
0.0
>>> f(0, 0)
1.0
>>> sys.float_info.epsilon
2.220446049250313e-16
>>> f(0, _)
0.9999999999999999

pyibl.bounded_quadratic_similarity(minimum, maximum)

Returns a function of two arguments that returns a similarity value reflecting a quadratic scale between minimum and maximum. Both arguments to the function returned should be Real numbers between minimum and maximum, inclusive. If the two arguments to the function returned are equal they are maximally similar, and one is returned. If the absolute value of their difference is as large as possible, they are maximally different, and zero is returned. Otherwise a scaled value on a quadratic scale between these two extrema, measuring the magnitude of the difference between the arguments to the returned function is used, a value between zero and one being returned.

Raises a ValueError if either minimum or maximum is not a Real number, or if minimum is not less than maximum.

When the returned function is called if either of its arguments is not a Real number a ValueError is then raised. If either of those arguments is less than minimum, or greater than maximum, a warning is issued, and either minimum or maximum, respectively, is instead used as the argument’s value.

>>> f = bounded_quadratic_similarity(-1, 1)
>>> f(0, 1)
0.25
>>> f(-0.1, 0.1)
0.81
>>> f(-1, 1)
0.0
>>> f(0, 0)
1.0
>>> sys.float_info.epsilon
2.220446049250313e-16
>>> f(0, _)
0.9999999999999998

Internals

PyIBL is built on top of PyACTUp, a Python implementation of a portion of ACT-R’s declarative memory. This chapter describes the computations underlying decisions made by PyIBL, which are mostly carried out in the underlying PyACTUp code.

The fundamental unit of memory in PyIBL is an instance (a “chunk” in PyACTUp), which combines the attributes of a choice with the result it led to, along with timing data.

Activation

A fundamental part of retrieving an instance from an agent’s memory is computing the activation of that instance, a real number describing how likely it is to be recalled, based on how frequently and recently it has been experienced by the Agent, and how well it matches the attributes of what is to be retrieved.

The activation, 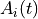of instance i at time t is a sum of three components,

the base-level activation, the partial matching correction, and the activation noise.

Base-level activation

The base-level activation, 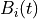, describes the frequency and recency of the instance i, and depends upon the decay parameter of the Agent, d. In the normal case, when the agent’s optimized_learning parameter is False, the base-level activation is computed using the amount of time that has elapsed since each of the past experiences of i; in the following this set of times of experiences of i before t is denoted by .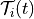

If the agent’s optimized_learning parameter is True an approximation is used instead, sometimes less taxing of computational resources. It is particularly useful if the same instances are expected to be seen many times, and assumes that repeated experiences of the various instances are distributed roughly evenly over time. Instead of using the times of all the past occurrences of i, it uses 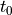, the time of the first appearance of i, and 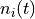, a count of the number of times i has appeared before time t.

The optimized_learning parameter may also be set to a positive integer. This specifies a number of most recent reinforcements of a chunk to be used to compute the base-level activation in the normal way, with the contributions of any older than those approximated using a formula similar to the preceding.

Note that setting the decay parameter to None disables the computation of base-level activation. That is, the base-level component of the total activation is zero in this case.

Partial Matching

If the agent’s mismatch_penalty parameter is None, the partial matching correction, 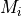, is zero. Otherwise 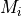depends upon the similarities of the attributes of the instance to those attributes being sought in the retrieval and the value of the mismatch_penalty parameter.

PyIBL represents similarities as real numbers between zero and one, inclusive, where two values being completely similar, ==,, has a value of one; and being completely dissimilar has a value of zero; with various other degrees of similarity being positive, real numbers less than one.

How to compute the similarity of two instances is determined by the programmer, using the method similarity(). A function is supplied to this method to be applied to values of the attributes of given names, this function returning a similarity value. In addition, the similarity method can assign a weight, 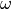, to these attributes, allowing the mismatch contributions of multiple attributes to be scaled with respect to one another. If not explicitly supplied this weight defaults to one.

If the mismatch parameter has positive real value 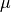, the similarity of attribute j of instance i to the desired value of that attribute is 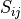, the similarity weight of attribute j is 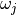, and the set of all attributes for which a similarity function is defined is 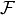, the partial matching correction is

The value of 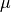should be positive, and thus 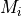is negative, so it is not so much that increased similarities increase the activation as dissimilarities reduce it, and increased similarities simply cause it to be reduced less, scaled by the value of .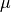

Attributes for which no similarity function is defined are always matched exactly, non-matching instances not being considered at all.

Activation noise

The activation noise, , implements the stochasticity of retrievals from an agent’s memory. It is sampled from a distribution, scaled by the noise parameter. This sampling occurs every time the activation of an instance needs to be calculated, and is typically different each time.

By default this distribution is a logistic distribution centered on zero. The distribution used can be changed for special purposes by using an Agent’s noise_distribution attribute, though for nearly all uses the default is the right choice.

An Agent has a scale parameter, noise. If this parameter is denoted as 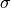, and if the value sampled from the distribution is 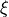, the activation noise is

Note that setting the noise parameter to zero results in supplying no noise to the activation. This does not quite make operation of PyIBL deterministic, since retrievals of instances with the same activations are resolved randomly.

Blending

Once the activations of all the relevant instances have been computed, they are used to compute a blended value of the utility, an average of the utilities of those instances weighted by a function of the instances’ activations, the probability of retrieval.

A parameter, the temperature, or 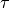, is used in constructing this blended value. In PyIBL the value of this parameter is by default the noise parameter used for activation noise, multiplied by 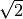. However it can be set independently of the noise, if preferred, and is often set to 1.

For a given option being considered, k, let 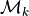be the set of all matching instances. Then the probability of retrieval of instance 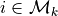at time t is

From these we can compute the blended value at time t, 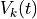of this option’s various utilities in the instances for this option. If 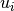is the utility that was provided as the first argument in the call to respond() that completed the experience of instance i, or equivalently was supplied by a call to populate() or with the default_utility, this blended value is

Changes to PyIBL

Changes between versions 5.1.1 and 5.1.3

• added noise_distribution

Changes between versions 5.1 and 5.1.1

• Fixed a bug which caused some rows to be omitted from the aggregate_details; since the plot() method depends upon the aggregate_details plots weere sometimes incorrect, too.

Changes between versions 5.0.4 and 5.1

• Add the aggregate_details attribute.

• Add the plot() method.

Changes between versions 5.0.2 and 5.0.4

• The sequence of all attribute names is now a tuple of strings rather than a list.

Changes between versions 5.0.1 and 5.0.3

• Add further information to trace output.

• Update some copyrights and documentation.

Changes between versions 5.0 and 5.0.1

• Update copyrights, documentation and dependencies.

• Fix a bug afflicting tracing when noise is zero.

Changes between versions 4.2 and 5.0

• PyIBL now requires Python 3.8 or later.

• Substantial changes were made to the internal representations of agents and instances enabling faster IBL computations in many use cases involving large numbers of instances.

• Agent attributes can now be any non-empty string, and the arguments to the Agent constructor are now in a different order.

• Changed the arguments to choose(), populate() and forget().

• Similarity functions are now per-Agent instead of global, and are set with the similarity() method.

• Similarities can now have weights, also set with the similarity() method, allowing easier balancing of the contributions of multiple attributes.

• The advance() method has been added to the API.

• The choose2() method has been replaced by an optional argument to choose().

• The populate_at() method has been replaced by an optional argument to populate().

• There is a new method discrete_blend() useful for creating models using a different paradigm from PyIBL’s usual choose()/respond() cycle.

• It is now possible to set optimized_learning as an Agent parameter in the usual way, instead of as an argument to reset(). In addition, optimized_learning can now take positive integers as its value, enabling a mixed mode of operation.

• The default value of default_utility_populates is now False, and it can be set at Agent creation time with an argument to the constructor.

• There is a new Agent property, fixed_noise, allowing a variant noise generation scheme for unusual models.

• General tidying and minor bug fixes.

When upgrading existing version 4.x models to version 5.0 or later some syntactic changes will nearly always have to be made. In particular, PyIBL no longer abuses Python’s keyword arguments, and lists of choices now need to be passed to choose() and populate(), which now also take their arguments in a different order. In simple cases this is as easy as surrounding the formerly trailing arguments by square bracket, and swapping the result two arguments. For more complex cases it may be necessary to pass a list of dictionaries. For example, what in version 4.x would have been expressed as

a.populate(10, "red", "blue")
a.choose("red", "blue")

could be expressed in version 5.0 as

a.populate(["red", "blue"], 10)
a.choose(["red", "blue"])

If you are using partial matching you will also have to replace calls to the similarity() function by the Agent’s similarity() method. This method also takes slightly different arguments than the former function. For example, what in version 4.x would have been expressed as

similarity(cubic_similarity, "weight", "volume")

could be expressed in version 5.0 as

a.similarity(["weight", "volume"], cubic_similarity)

Changes between versions 4.2 and 4.2.0.1

• PyIBL is now distributed via PyPi and need no longer be downloaded from the DDMLab website.

Changes between versions 4.1 and 4.2

• The choose2() method has been added to the API.

• The respond() method now takes a second, optional argument.

• There is more flexability possible when partially matching attributes.

• PyIBL now requires Pythonn verison 3.7 or later.

• General tidying and minor bug fixes.

Changes between versions 4.0 and 4.1

• The API for DelayedFeedback has been changed.

• The reset() now has an additional, optional argument, preserve_prepopulated.

• Some minor bug fixes.

Changes between versions 3.0 and 4.0

• Situations and SituationDecisions are no longer needed. Choices are now ordinary Python objects, such as dicts and lists.

• The overly complex logging mechanism was a rich source of confusion and bugs. It has been eliminated, and replaced by a simpler mechanism, details, which facilitates the construction of rich log files in whatever forms may be desired.

• Populations were rarely used, badly understood and even when they were used were mostly just used to facilitate logging from multiple agents; in version 4.0 populations have been eliminated, though they may come back in a different form in a future version of PyIBL.

• Methods and attributes are now uniformly spelled in snake_case instead of camelCase.

• Many attributes of Agents can now be specified when they are created.

• Similarities are now shared between Agents, by attribute name, rather than being specific to an Agent.

• Several common similarity functions are predefined.

• The current time can now be queried.

• Delayed feedback is now supported.

• PyIBL is now built on top of PyACTUp.

• Some bugs have been fixed, and things have been made generally tidier internally.

Changes between versions 2.0 and 3.0

• Similarity and partial matching are now implemented.

• SituationDecisions have changed completely, and are no longer created by an Agent.

• Logging has changed substantially: there can be multiple, differently configured logs; it is now possible to have per-Agent logs, not just Population-wide logs; and logging configuration now controls not just which columns are shown, but the order in which they appear.

• Default values of noise and decay are now 0.25 and 0.5, respectively, matching oral common practice in ACT-R, instead of ACT-R’s out of the box defaults, which are rarely useful.

• General internal tidying

  Warning

  Note that version 3.0 was never publicly released though preliminary internal development versions of it were used for a variety of experiments, both within the DDMLab and elsewhere.

Changes between versions 1.0 and 2.0

• Agents are now publicly visible objects that can be passed around and moved from one Population to another. The API has completely changed so that you no longer cite an agent by name in a Population.

• Options presented to Agents are no longer merely decisions, but include situations as well.

• Logging is configured with strings rather than constants.

• Logging can now be configured to include or exclude unused options and instances.

• Bug fixes, particularly in logging.

• Better documentation.

• General internal tidying